Rekursif
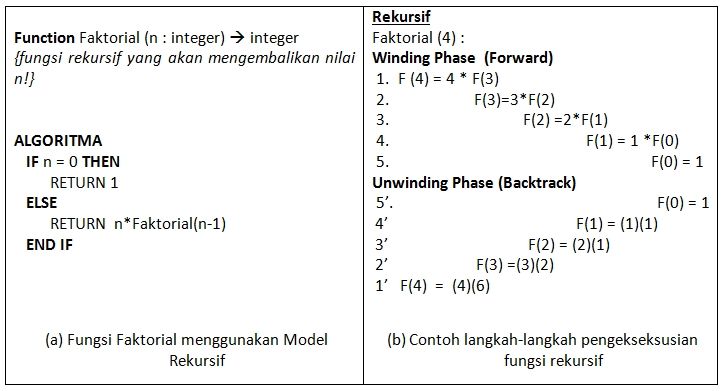
Suatu obyek mengikuti pola rekursif bilamana obyek itu dapat didefinisikan menjadi lebih sederhana dalam terminologi obyek itu sendiri. Pada pemrograman dan algoritme, prosedur dan fungsi yang bersifat rekursif akan memiliki 2 bagian yang penting yaitu bagian basis dan bagian rekurens. Bagian basis dari prosedur dan fungsi yang bersifat rekursif akan memiliki kegunaan sebagai bagian yang akan menghentikan proses rekursif serta akan mengembalikan suatu nilai yang terdefinisi. Bagian Rekurens dari prosedur dan fungsi yang bersifat rekursif akan memiliki kegunaan untuk memanggil kembali fungsi atau prosedur itu sendiri. Contoh klasik dari fungsi yang bersifat rekursif adalah fungsi faktorial. Gambar 1 menunjukkan bagian basis dan bagian rekurens dari fungsi faktorial.
Pada saat suatu fungsi yang bersifat rekursif dieksekusi maka dimungkinkan terdapat 2 fase dalam pemrosesan fungsi rekursif tersebut. Kedua fase yang mungkin terdapat dalam pemrosesan dan pengeksekusian fungsi rekursif tersebut adalah fase forward (winding phase) dan fase backtrack (unwinding phase). Gambar 2 menunjukkan algoritme fungsi faktorial dan proses pengeksekusiannya yang menggunakan 2 fase yaitu fase forward dan fase backtrack.
Jika dilihat dari tingkat pertumbuhan pemanggilan fungsi yang bersifat rekursif, maka fungsi rekursif dapat dibedakan menjadi 2 jenis yaitu Linear Recursion dan Tree Recursion. Fungsi Faktorial yang bersifat rekursif adalah salah satu contoh dari Linear Recursion, sedangkan Fungsi Pengurutan QuickSort yang bersifat rekursif adalah contoh dari Tree Recursion.
Quicksort
Algoritme fungsi pengurutan quicksort yang bersifat rekursif adalah salah satu contoh dari jenis fungsi rekursif Tree Recursion. Quicksort dalam memecahkan permasalah pengurutan akan menerapkan prinsip divide and conquer. Tahapan pengurutan pada algoritme quicksort untuk mengurutkan suatu array P yang elemen-elemennya bertipe bilangan bulat, akan mengikuti tahapan sebagai berikut :
- menentukan sebuah elemen dari array P tersebut yang akan disebut sebagai elemen pivot. Salah satu elemen pivot yang umum digunakan adalah elemen terakhir dari array P tersebut, dimana jika r adalah indeks terakhir dari array P, maka P[r] adalah elemen pivot.
- memecah dan mempartisi array P menjadi 2 sub array yaitu P[1 .. (s-1)] dan P[(s+1) .. (r-1)]. Proses pemecahan ini dilakukan dengan memperhatikan aturan sebagai berikut :
- Nilai dari elemen-elemen array P[1 .. (s-1)] ≤ P[r]
- Nilai dari elemen-elemen array P[(s+1) .. (r-1)] > P[r]
- Jika array P sudah terbagi menjadi 2 bagian, maka P[r] dapat disisipkan di indeks s
- Proses dan tahapan diatas harus terus berulang dan dilakukan secara rekursif untuk setiap sub array hasil pemartisian yang masih memiliki elemen dan baru dihentikan bila sub array hasil pemartisian sudah tidak memiliki elemen lagi.
Gambar 3 menunjukkan contoh langkah-langkah algoritme quicksort untuk melakukan pemecahan suatu array P yang berisi elemen - elemen bertipe bilangan bulat [45, 26, 77, 22, 120, 210, 100, 36] menjadi 2 sub array dan menyisipkan elemen pivot di posisi yang benar.










