kembali ke permasalahan rambatan panas tadi maka turunan pertama ini asumsi fisisnya adalah perubahan suhu benda terhadap waktu sedangkan turunan kedua ini adalah tanda "dimulainya" perubahan suhu pada benda tersebut dengan parameter "seberapa besar percepatan yang cukup (atom itu bertambah cepat getaranya/ berubah kecepata nya terhadap waktu) untuk dapat menghasilkan perubahan suhu pada lempengan logam 2 dimensi tersebut.
Solusi umum dari permasalahan umum ini adalah persamaan gelombang, entah berupa gelombang sinusoidal (gelombang periodik/ gelombang naik turun yang terus berulang) ataupun gelombang eksponensial (gelombang yang mempunyai fungsi kenaikan ke titik puncak atau titik terdalam secara eksponensial) karena memang pergerakan partikel tersebut diasumsikan secara matematis model pergerakan atau rambatan panasnya seperti gelombang (nanti mungkin ada sesi pembahasan hubungan antara fungsi gelombang sinusoidal dan fungsi eksponensial) yang bisa kita lihat pada gambar dibawah ini (fyi, ini gambar penerapan operator laplacian (yang konsepnya sama dengan penerapanya dipermasalahan perambatan panas pada penampang logam ini) sebagai operator pengolahan citra menggunakan aplikasi yang bisa mengolah data citra). Sebenarnya ada lagi bentuk lainya yaitu bentuk gelombang sinusoidal hiperbolik, dimana pada umumnya sama saja bentuknya namun gelombang sinusoidal hiperbolik ini mewakili 2 bentuk gelombang eksponensial dan sinusoidal sekaligus (mungkin kita akan bahas nanti)
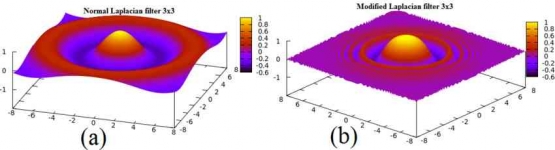
Nah kan kita kan sudah tahu nih model gerakan atom/ perambatan panasnya gimana, selanjutnya kita memasukkan model perambatan panas tersebut ke dunia nyata, memberi batasan atau nilai pada asumsi matematis model yang dibuat tersebut sehingga sesuai dengan keadaan yang bisa diterima lempengan panas tersebut, mungkin bahasa lainya memberi batasan terhadap ekspetasi diri dalam menentukan goal yang akan dicapai agar sesuai dengan kemampuan diri. Syarat batas yang kita gunakan dalam permasalahan ini sebagai berikut :
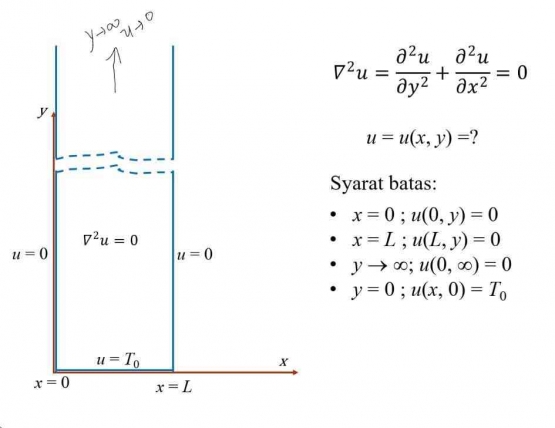
dengan u = f(x) = suhu pada lempeng logam 2 dimensi
di sini nilai u semuanya 0 kecuali pada syarat batas nilai y 0 atau pada dasar penampang logam dan x adalah nilai sesuatu (x
Apakah masalah penentuan perambatan panas sudah selesai? tentu saja belum, penggambaran rambatan panas dengan gelombang sinusoidal-eksponensial dengan batasanya tadi hanya untuk menggambarkan satu titik partikel atom pada lempeng logam, tentu saja kita ingin mengetahui keadaan semua titiknya, untuk itu kita menggunakan operator matematika integral dan sum (penjumlahan total), kita menggunakan operator matematika integral untuk menentukan jumlah keseluruhan perubahan suhu (distribusi suhunya) pada lempeng logam yang homogen dan operator matematika sum untuk menentukan jumlah keadaan atom (distribusi atomnya) disetiap titik logam yang tidak homogen (logam dianggap memiliki struktur atom yang berbeda-beda diberbagai titik logam sehingga keadaannya ketika menerima gangguan dari luar responya akan berbeda-beda), dengan menyelesaikan operasi matematika keduanya maka kita mengetahui bagaimana menggambarkan keadaan fisika yang ada didalam lempeng logam menggunakan matematika.

Pada gambar diatas, To adalah Suhu awal dengan batas integral 0 artinya pada suhu di x = 0 sampai didinding atau x = P














