Sistem Persamaan Linier Dua Variabel

 A. Pengertian PLDV

Persamaan linear dua variabel ialah persamaan yang mengandung dua variabel dimana pangkat/derajat tiap-tiap variabelnya sama dengan satu.

Bentuk umum :

ax + by = c

Keterangan:

a = Koefisien x

b = koefisien y

c = konstanta.

y dan x = Variabel

Contoh:

1. 4x + 5y = 20                             3. 2x -- 6y = 12

2. 2x -- 6y = 24                            4. 3x = y -- 7

B. Sistem Persamaan Linear Dua Variabel

Sistem persamaan linear dua variabel adalah dua persamaan linear dua variabel yang mempunyai hubungan diantara keduanya dan mempunyai satu penyelesaian.

Bentuk umum :

ax + by = c

px + qy = r

a, b, p, q disebut koefisien

c, r disebut konstanta.

y dan x disebut Variabel

C. Menyelesaikan Sistem Persamaan Linear Dua Variabel

Cara penyelesaian SPLDV dapat dilakukan dengan cara:

1. Substitusi

Menggantikan satu variabel dengan variabel dari persamaan yang lain.

Contoh:

Carilah penyelesaian sistem persamaan

x + 2y = 8 dan 2x – y = 6

Jawab:

Kita ambil persamaan pertama yang akan disubstitusikan yaitu x + 2y = 8

Kemudian persamaan tersebut kita ubah menjadi x = 8 – 2y, Kemudian persamaan yang diubah tersebut disubstitusikan ke persamaan 2x – y = 6 menjadi :

2 (8 – 2y) – y = 6 → (x persamaan kedua menjadi x = 8 – 2y)

16 – 4y – y = 6

16 – 5y = 6

-5y = 6 – 16

-5y = -10

5y = 10

y = 10 : 5

y = 2

masukkan nilai y = 2 ke dalam salah satu persamaan :

x = 8 – 2y

x = 8 – 2(2)

x = 8 – 4

x = 4

Jadi penyelesaian dari sistem persamaan linear dua variabel x + 2y = 8 dan 2x – y = 6 adalah x = 4 dan y = 2.

2. Eliminasi

Eliminasi dilakukan dengan cara menghilangkan salah satu variabel x atau y dari dua persamaan.

Contoh:

Carilah penyelesaian sistem persamaan

x + 2y = 8 dan 2x – y = 6

Jawab:

(i) mengeliminasi variabel x

sumber gambar: dokumen pribadi

sumber gambar: dokumen pribadi

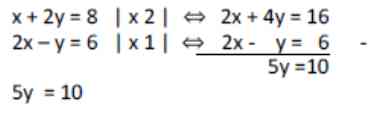
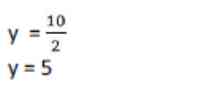
(ii) mengeliminasi variabel y

sumber gambar: dokumen pribadi

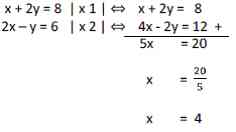
Jadi penyelesaian dari sistem persamaan x + 2y = 8 dan 2x – y = 6 adalah x = 4 dan y = 2.

* catatan

nilai + atau – digunakan untuk menghilangkan/eliminasi salah satu variable agar menjadi 0

Contoh di atas:

(i) yang dieliminasi adalah x :

x dalam persamaan satu + dan persamaan dua + , untuk eliminasi digunakan tanda –

(ii) yang dieliminasi adalah y :

y dalam persamaan satu +, persamaan dua - , untuk eliminasi digunakan tanda +

3. Grafik

Dengan menggambarkan persamaan linearnya pada koordinat Cartesius, titik potong dari kedua persamaan linier tersebut merupakan penyelesaiannya.

Contoh:

Carilah penyelesaian dari:

x + y = 8 dan 2x – y = 4

Jawab:

• Tentukan titik potong garis x + y = 8 dengan sumbu x dan sumbu y

titik potong dengan sumbu y jika x = 0

jika x = 0 → maka y = 8 – x = 8 – 0 = 8

titik potong dengan sumbu x jika y = 0

jika y = 0 → x = 8 – y = 8 – 0 = 8

Maka persamaan garis x + y = 8 adalah melalui titik (0.8) dan (8,0).

• Tentukan titik potong garis 2x – y = 4 dengan sumbu x dan sumbu y

titik potong dengan sumbu y jika x = 0

jika x = 0 → maka y = 2x – 4 = 2(0) – 4 = 0 - 4 = - 4

titik potong dengan sumbu x jika y = 0

jika y = 0 → 2 x = y + 4 = 0 + 4 = 4, maka x = 2

Maka persamaan garis 2x – y = 4 adalah melalui titik (0, -4) dan (2,0).

Gambar grafiknya sebagai berikut:

sumber gambar: dokumen pribadi

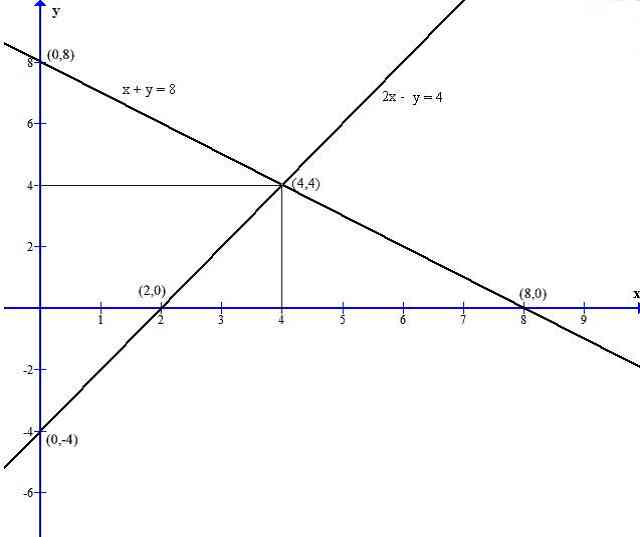
dari gambar grafik terlihat titik potong garis x + y = 8 dan 2x – y = 4 adalah (4,4).

Jadi penyelesaian dari x + y = 8 dan 2x – y = 4 adalah x = 4 dan y = 4.

Contoh penggunaan SPLDV dalm kehidupan sehari-hari:

1. Harga 2 kg salak dan 3 kg jeruk adalah Rp32.000,00, sedangkan harga 3 kg salak dan 2 kg jeruk adalah Rp33.000,00. Harga 1 kg salak dan 5 kg jeruk adalah ....

Jawab:

Harga 2 kg salak dan 3 kg jeruk adalah Rp32.000,00, sedangkan harga 3 kg salak dan 2 kg jeruk adalah Rp33.000,00.

Dari permasalahan di atas, dapat diperoleh sistem persamaan linear berikut.

Misalkan: harga 1 kg salak dilambangkan s; harga 1 kg jeruk dilambangkan j.

sumber gambar: dokumen pribadi

sumber gambar: dokumen pribadi

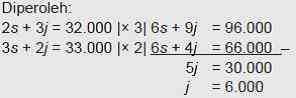
Harga 1 kg salak dan 5 kg jeruk adalah 

= Rp7.000,00 + 5 x Rp6.000,00

= Rp37.000,00

2. Harga 2 buah mangga dan 3 buah jeruk adalah Rp6000, kemudian apabila harga untuk membeli 5 buah mangga dan 4 buah jeruk adalah Rp11.500,- Berapa jumlah uang yang harus dibayar apabila kita akan membeli 4 buah manga dan 5 buah jeruk ?

Jawab :

Dalam menyelesaikan soal cerita seperti di atas diperlukan penggunaan model matematika.

Misal: harga 1 buah mangga adalah x dan harga 1 buah jeruk adalah y

Maka model matematika soal tersebut di atas menjadi :

2x + 3 y = 6000

5x + 4 y = 11500

Ditanya 4 x + 5 y = ?

Kita eliminasi variabel x :

sumber gambar: dokumen pribadi

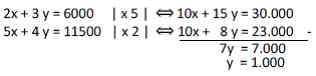
Substitusi ke dalam salah satu persamaan :

2x + 3 y = 6000

2x + 3 . 1000 = 6000

2x + 3000 = 6000

2x = 6000 – 3000

2x = 3000       → x = 1500

didapatkan x = 1500 (harga sebuah mangga) dan y = 1000 (harga sebuah jeruk) sehingga uang yang harus dibayar untuk membeli 4 buah mangga dan 5 buah jeruk adalah

4 x + 5 y

= 4 x 1500 + 5 x 1000

= 6000 + 5000

= Rp11.000,-

Sebagai bahan latihan soal bisa diunduh Disini.

Semoga bermanfaat. Terima Kasih.