A. Relasi
Relasi bisa diartikan sebagai suatu aturan yang menghubungkan anggota daerah asal (domain) dan anggota daerah kawan (kodomain). Dalam relasi, tidak ada aturan khusus yang harus dipenuhi untuk memasangkan anggota himpunan daerah asal ke anggota himpunan daerah kawan.
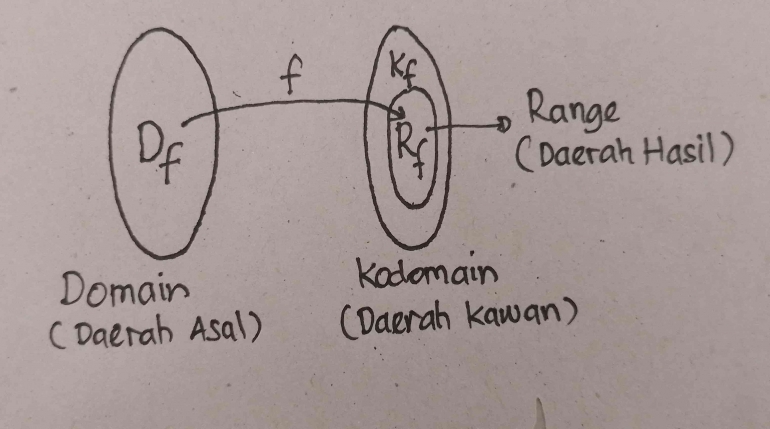
Setiap anggota himpunan daerah asal bisa mempunyai pasangan lebih dari satu atau boleh juga tidak memiliki pasangan sama sekali. Relasi dari dua buah himpunan dapat dinyatakan dengan tiga cara yaitu:
- Diagram panah
Diagram panah merupakan cara yang paling mudah dalam menyatakan suatu relasi. Diagram ini akan membentuk pola dari suatu relasi ke dalam bentuk gambar arah panah yang menyatakan hubungan dari anggota himpunan A ke anggota himpunan B.
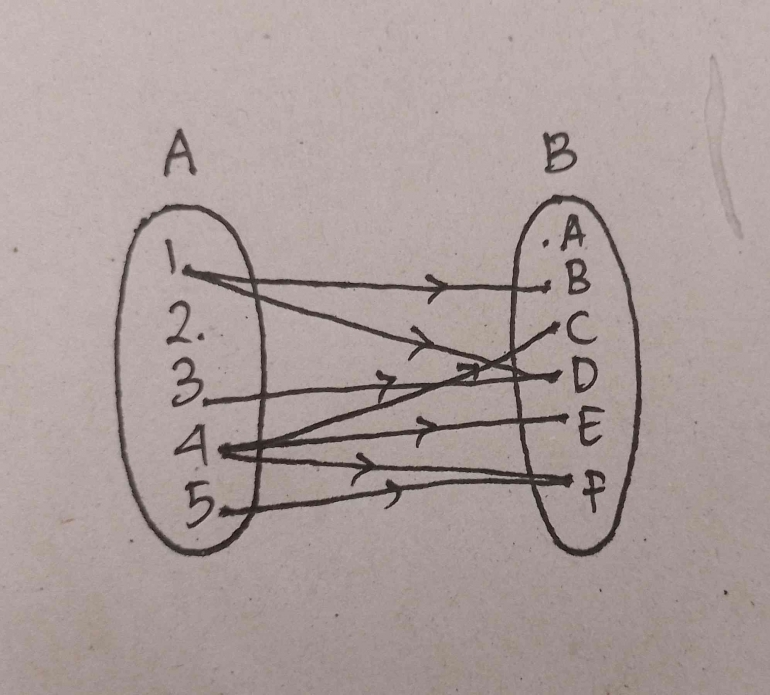
- Diagram Cartesius
Diagram Cartesius adalah sebuah diagram yang terdiri dari sumbu X dan sumbu Y. Dalam diagram Cartesius, anggota himpunan A terletak pada sumbu X, sedangkan anggota himpunan B terletak pada sumbu Y. Relasi yang menghubungkan himpunan A ke B ditunjukkan dengan noktah ataupun titik.
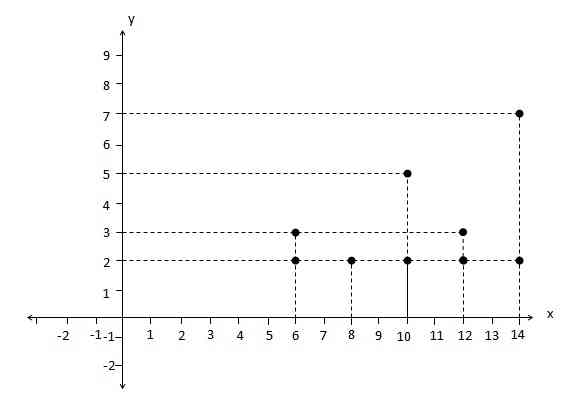
- Himpunan Pasangan Terurut
Sebuah relasi yang menghubungkan satu himpunan ke himpunan lainnya bisa disajikan dalam bentuk himpunan pasangan berurut. Cara penulisannya yaitu anggota himpunan A ditulis pertama, sedangkan anggota himpunan B yang menjadi pasangannya ditulis kedua.
Contohnya seperti ini:
Himpunan A = {Indonesia, Jepang, Korea, Perancis}. Himpunan B = {Tokyo, Paris, Jakarta, Seoul}. Tentukan himpunan pasangan berurut dari negara dan ibu kotanya.
Jawaban:
{(Indonesia,Jakarta), (Jepang,Tokyo), (Korea,Seoul), (Perancis,Paris)}
B. Fungsi
Fungsi atau pemetaan merupakan relasi khusus dari himpunan A ke himpunan B, dengan aturan setiap anggota himpunan A dipasangkan tepat satu ke anggota himpunan B. Semua anggota himpunan A atau daerah asal disebut dengan domain, sedangkan semua anggota himpunan B atau daerah kawan disebut kodomain. Fungsi dapat dinyatakan dalam bentuk diagram panah, himpunan pasangan berurut dan diagram Cartesius.
Untuk memahaminya lebih lanjut, perhatikan gambar di bawah. Himpunan A atau daerah asall disebut dengan domain. Himpunan B yang merupakan daerah kawan disebut kodomain. Anggota daerah kawan yang merupakan hasil dari pemetaan disebut daerah hasil atau range fungsi. Jadi dari diagram panah di atas dapat disimpulkan bahwa Domain (Df) adalah A = {1,2,3} Kodomain adalah B = {1,2,3,4} Range/Hasil (Rf) adalah = {2,3,4}
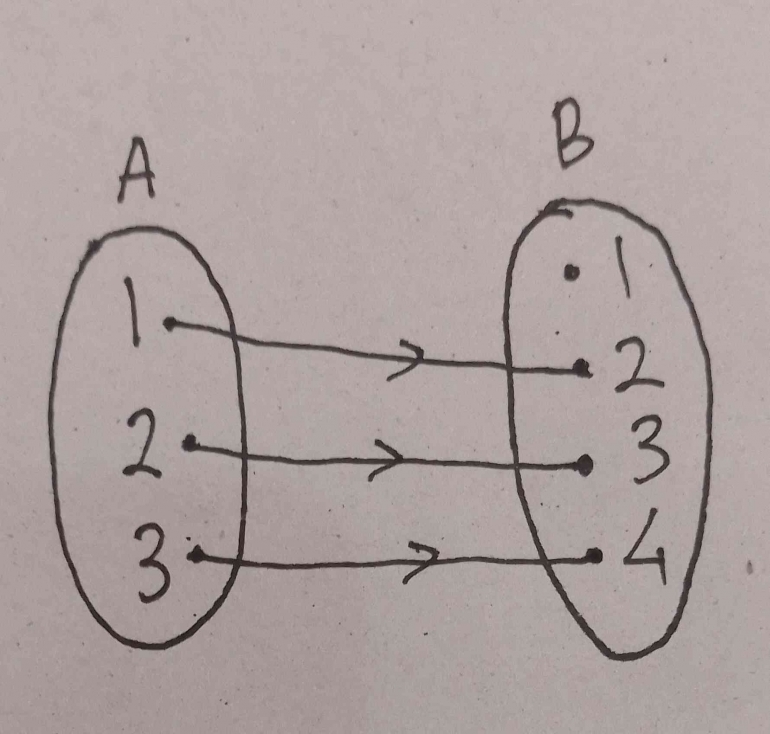
Banyak pemetaan yang dapat terjadi :
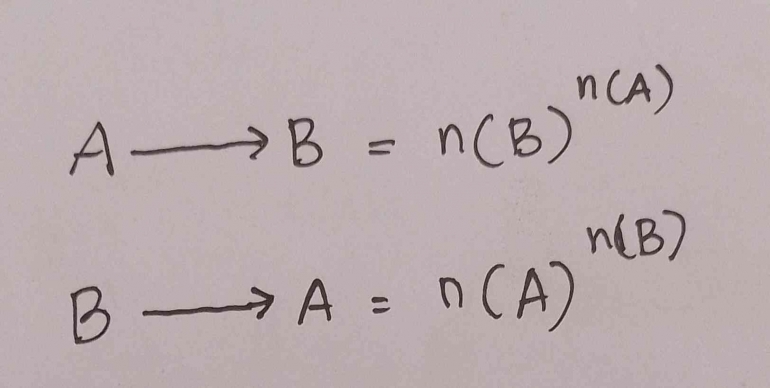
Keterangan:
n(A) = jumlah anggota himpunan A
n(B) = jumlah anggota himpunan B
C. Notasi Fungsi
Fungsi dapat dinotasikan dengan huruf kecil seperti f, g, h, i, dan sebagainya. Fungsi f memetakan himpunan A ke himpunan B, maka dapat dinotasikan dengan f(x):A→B.
Contohnya adalah fungsi f yang memetakan A ke B dengan aturan f : x → 2x + 2. Dari notasi fungsi tersebut, x adalah anggota domain. Fungsi x → 2x + 2 memiliki arti bahwa fungsi f memetakan x ke 2x + 2. Jadi daerah hasil x oleh fungsi f adalah 2x + 2. Jadi kamu bisa menotasikannya menjadi f(x) = 2x +2. Jika fungsi f:x → ax + b dengan x anggota domain f, maka rumus fungsi f adalah f(x) = ax +b.
Contoh:
1. Diketahui fungsi f:x → 2x – 2 dengan x bilangan bulat. Tentukan nilai dari f(3)!
Jawab:
Fungsi f:x → 2x – 2 dapat dinyatakan dengan f(x) = 2x – 2 sehingga,
f(x) = 2x – 2
f(3) = 2(3) – 2 = 4
2. Jika f(x) = 3x – 2 dan f(a) = 19. Maka nilai a adalah …
Jawab:
F(x) = 3x – 2, maka f(a) = 3a – 2
F(a) = 19
3a – 2 = 19
3a – 2 + 2 = 19 + 2 …………………………….. kedua ruas ditambah 2
3a = 21
3a : 3 = 21 : 3 ……………………………… kedua ruas dibagi 3
a = 7
3. Diketahui fungsi f(x) = 2x + 3. Jika f(k) = 9, tentukan nilai k.
Jawab:
f(x) = 2x + 3
f(k) = 2(k) + 3 = 9
2k = 9 – 3
2k = 6
k = 3
D. Korespondensi Satu-Satu
Suatu relasi khusus yang menghubungkan setiap anggota domain dengan tepat satu anggota kodomain, dan setiap anggota kodomain berpasangan dengan satu anggota domain.
Syarat :
n(Domain) = n(Kodomain)
Domain dan kodomain tepat berpasangan satu – satu, dan semua anggota habis dipasangkan.
Banyak korespondensi satu-satu yang mungkin :
n(A) = n(B), sehingga A→B = B→A
n(A)! Atau n(B)!
! = faktorial
Contoh. 4! = 4 x 3 x 2 x 1 = 24
Contoh:
Jika A = {2,3,5,7} dan B = {p, q, r, s}. Banyaknya korespondensi satu-satu yang terbentuk ada ... cara
Jawab:
Banyak korespondensi satu-satu yang mungkin :
= n(A)!
= 4!
= 4 x 3 x 2 x 1
= 24
Baca konten-konten menarik Kompasiana langsung dari smartphone kamu. Follow channel WhatsApp Kompasiana sekarang di sini: https://whatsapp.com/channel/0029VaYjYaL4Spk7WflFYJ2H














