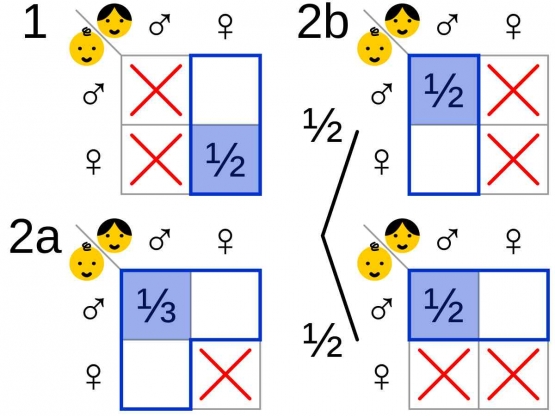
Analisis: Probabilitasnya sebenarnya adalah 2/3. Ini karena dari empat kemungkinan kombinasi (BB, BG, GB, GG), hanya tiga kombinasi yang memenuhi syarat bahwa setidaknya satu anak adalah laki-laki (BB, BG, GB). Dari tiga kombinasi ini, dua dari mereka melibatkan satu laki-laki dan satu perempuan (BG, GB).
3. Paradoks Pemilihan Ulang (Election Paradox)
Paradoks ini muncul ketika kita mempertimbangkan preferensi mayoritas dalam sebuah pemilihan.
Pertanyaan: Dalam sebuah pemilihan dengan tiga kandidat (A, B, C) dan tiga pemilih dengan preferensi berbeda, apakah mungkin terjadi situasi di mana setiap kandidat bisa dikalahkan oleh kandidat lainnya dalam pemungutan suara langsung?
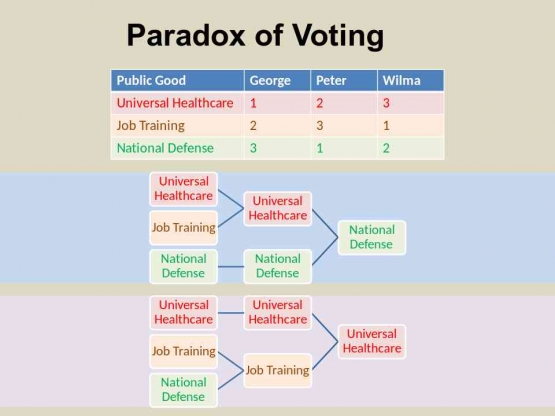
Contoh: Jika preferensi pemilih adalah sebagai berikut:
- Pemilih 1: A > B > C
- Pemilih 2: B > C > A
- Pemilih 3: C > A > B
Analisis: Dalam skenario ini:
- A kalah dari B (2 pemilih lebih suka B daripada A)
- B kalah dari C (2 pemilih lebih suka C daripada B)
- C kalah dari A (2 pemilih lebih suka A daripada C)
Ini menunjukkan bahwa tidak ada pemenang yang jelas, meskipun setiap kandidat bisa dikalahkan oleh kandidat lain, menciptakan lingkaran preferensi yang tak pernah berakhir.
4. Paradoks Berkson (Berkson's Paradox)
Paradoks ini muncul dalam konteks statistik dan bias seleksi, yang terjadi ketika dua variabel tampak saling berhubungan secara negatif tetapi sebenarnya tidak, karena sampel yang diambil secara kondisional.










