Filsafat Matematika Descartes [3]

Ingatlah selain penekanannya pada gerakan "tepat dan tepat" yang dapat digunakan untuk menggambarkan kurva geometris yang sah, Descartes juga mengklaim kurva ini "dapat dipahami sebagai digambarkan oleh gerakan terus menerus atau dengan beberapa gerakan berturut-turut." seperti itu, cukup berharap konstruksi geometris dari kurva-kurva ini tidak boleh berjalan dengan cara yang sama seperti Buku Satu, di mana Descartes membangun kurva Pappus dengan menyelesaikan persamaan yang menjadi masalah pengurangan masalah tersebut. Namun, ketika Descartes memperlakukan Masalah Pappus lima baris dalam Buku Dua, ia sebenarnya menawarkan konstruksi titik-titik dari kurva Pappus. Dia kemudian menyatakan konstruksi searah dari kurva Pappus "geometris" ini sangat berbeda dari konstruksi searah kurva non-geometris, "mekanis":

Perlu dicatat ada perbedaan besar antara metode ini di mana kurva [Pappus] dilacak dengan menemukan beberapa titik di atasnya, dan yang digunakan untuk kurva spiral dan yang serupa. Dalam yang terakhir, tidak ada titik kurva yang diperlukan dapat ditemukan dengan senang hati, tetapi hanya titik-titik seperti yang dapat ditentukan oleh proses yang lebih sederhana daripada yang diperlukan untuk komposisi kurva ... Di sisi lain, tidak ada titik pada ini ["Geometris"] kurva yang memasok solusi untuk masalah yang diusulkan yang tidak dapat ditentukan oleh metode yang saya berikan (G, 88-91).

Saran dari Descartes adalah ketika secara searah membangun kurva geometris, dapat mengidentifikasi titik yang mungkin pada kurva, dan segera setelah pernyataan di atas, melanjutkan untuk menyamakan kurva yang dibangun dengan cara ini dengan kurva yang mungkin dapat dibangun dengan gerakan kontinu. : "Metode penelusuran kurva ini dengan menentukan sejumlah titik yang diambil secara acak hanya berlaku untuk kurva yang dapat dihasilkan oleh gerakan reguler dan kontinu" (G, 91).

Perbedaan antara konstruksi kurva "geometris" dan "mekanis" ini memiliki dua tujuan yang agak penting dalam program La Geometrie : (1) Descartes dapat menetapkan kurva Pappus yang telah ia buat secara pointwise sebenarnya adalah "geometris" dan dengan demikian lengkap sintesis (atau demonstrasi) dari Masalah Pappus umum, dan (2) ia dapat mempertahankan batas antara kurva "geometris" yang dapat dipahami dan kurva "mekanis" yang tidak dapat dipahami.

Tanpa indikasi yang jelas mengapa konstruksi kurva Pappus yang menunjuk ke titik adalah "geometris," Descartes harus membiarkan kurva "mekanis" seperti spiral dan quadratrix ke dalam domain kurva geometris, karena kurva ini juga dapat dibangun dengan cara yang tajam. Ingatlah misalnya konstruksi quadratrix yang menunjuk Clavius.

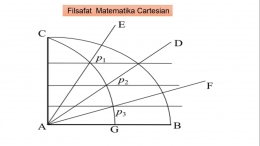
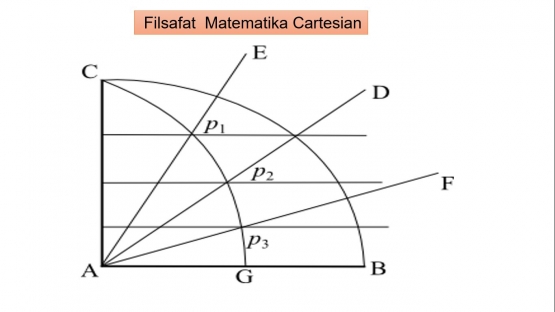
Menurut deskripsi Clavius, mulai dengan kuadran lingkaran dan kemudian mengidentifikasi titik-titik persimpangan antara segmen yang membagi dua kuadran dan segmen yang membagi dua busur kuadran. Yaitu, kami mengidentifikasi beberapa titik berpotongan segmen yang dapat dibangun dengan penggaris lurus dan kompas, dan kemudian, untuk menghasilkan quadratrix, kami menghubungkan titik-titik perpotongan, yang ditempatkan secara merata di sepanjang kurva yang dicari.

Mengapa konstruksi seperti itu tidak "geometris"? Karena, menurut Descartes, jika melanjutkan seperti Clavius, "tidak ada titik kurva yang diperlukan dapat ditemukan dengan senang hati." Secara khusus, mengingat pembatasan konstruksi Euclidean, hanya dapat membagi busur yang diberikan menjadi 2 bagian n . Dengan demikian, apa yang disarankan oleh Descartes adalah tidak mungkin untuk membagi busur dengan cara apa pun yang inginkan, dan oleh karena itu tidak dapat menemukan titik sembarang di sepanjang kurva dengan menggunakan konstruksi pointwise.

Namun dalam kasus kurva "geometrik", dapat menemukan titik sembarang pada kurva dengan mengajukan banding ke persamaan yang sesuai dengan masalah; atau meminjam terminologi Bos, Descartes mengklaim kurva "geometris", dan kurva Pappus pada khususnya, dapat dihasilkan oleh konstruksi "umum" yang mengarah ke titik.

(dok. pribadi)

Sementara pertimbangan konstruksi Clavius dari quadratrix menawarkan beberapa alasan untuk menerima perbedaan Descartes antara berbagai jenis konstruksi yang searah, masih ada klaim kontroversial kurva yang digambarkan oleh "generik" konstruksi searah adalah kurva yang dapat dibangun dengan gerakan kontinu. Identifikasi ini memungkinkan Descartes untuk menetapkan kurva Pappus sebagai kurva "geometris", tetapi ia tidak menawarkan bukti identitas, dan dengan demikian, ada pertanyaan apakah Descartes sebenarnya menunjukkan kurva Pappus "geometris" menurut standarnya sendiri. 

Ada pertanyaan lebih lanjut seputar kriteria Descartes untuk kurva "geometris". Seperti yang telah di lihat di atas, perhatian eksplisit Descartes dalam Buku Dua adalah untuk menawarkan standar untuk kurva geometris yang terikat dengan gerakan yang jelas, jelas dan berbeda yang diperlukan untuk konstruksi mereka.

Namun, baru-baru ini menawarkan kasus yang meyakinkan di balik pernyataan eksplisit Descartes di La Geometrie terdapat masalah yang lebih mendasar: Untuk memastikan kurva tersebut, para ahli matematika telah menggunakan untuk menyamakan lingkaran, seperti spiral dan quadratrix yang secara eksplisit disebutkan.